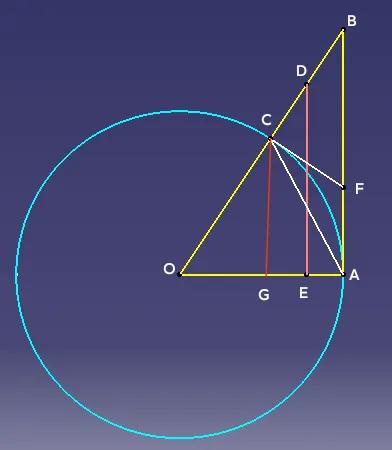
用面积法证明线段关系 如图,A为圆O上一点,过A点作圆O切线,B为切线上一点,OB交圆O于C点,D为BC中点,DE垂直OA于E,则DE>劣弧AC。 连接AC,过C作圆O切线,交AB于F,则∠BCE=90°,CF=FA。在RT△BCF中,BF>CF=FA。 所以S△BCF>S△CAF>S弓形AC,所以S△ABC>2S弓形AC。 又S△AOB+S△AOC=2S△AOC+S△ABC>2(S△AOC+S弓形AC)=2S扇形AOC 过C作CG⊥AO于G,则有S△AOB+S△AOC=(CG+AB)·AO/2=DE·AO,而S扇形AOC=OA·劣弧AC/2。根据上述关系可得:DE·AO>2·OA·劣弧AC/2,化简得:DE>弧AC