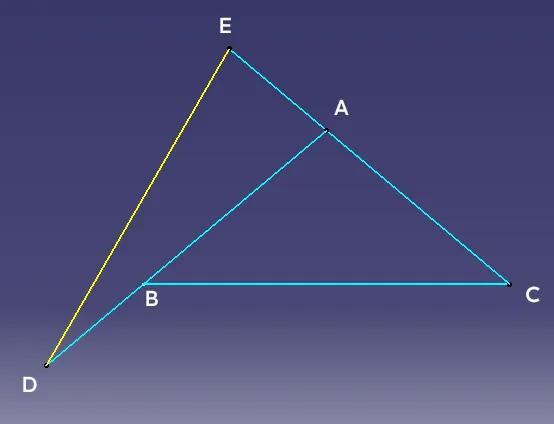
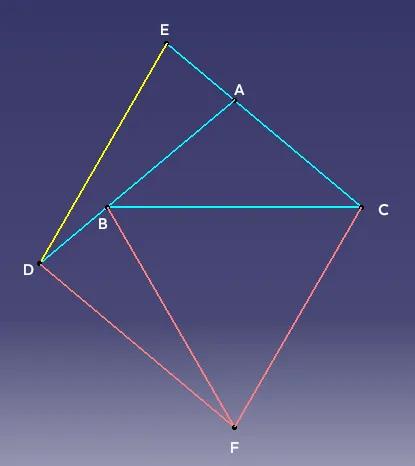
构造全等三角形解角度证明题 如图一,等腰△ABC中,延长边AB到D点,延长CA边到E点,连接DE,恰有AD=BC=CE=DE,求证∠BAC=100°。 证明如图二,根据题意∠DAE=∠DEA,且都为锐角,所以∠BAC=180°-∠DAE为钝角,所以△ABC中,有AB=AC(两个底角不可能为钝角)。 根据以上结论可得AE=CE-AC=AD-AB=BD。 以BD为底,作与△ADE全等的△BFD,连接CF,则有∠FDB=∠DAE,所以AD//EC(内错角相等),同时有FD=EC,所以四边形EDFC为平行四边形。 所以CF=DE=BF=BC,△BCF为等边三角形。 ∠DBF=∠DAE=2∠ABC,又∠ABC+∠CBF+∠DBF=180°,所以可得3∠ABC+60°=180°,∠ABC=40°,从而∠BAC=180°-2x40°=100°。