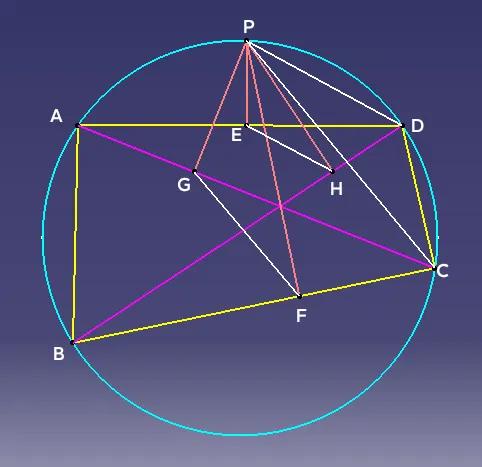
圆上任一点到其内接四边形对边距离之积等于这点到对角线距离之积 如图,四边形ABCD为圆内接四边形,P为圆上任一点,作PE⊥AD于E,PF⊥BC于F,PG⊥AC于G,PH⊥BD于H,则有PE·PF=PG·PH 连接PD、PC、EH、GF,根据题意易得PGFC四点共圆,PEHD四点共圆。 所以∠PFG=∠PCG=∠PCA=∠PDA =∠PDE=∠PHE。 ∠GPF=∠GCF=∠ACB=∠AOD =∠ADB=∠EDH=∠EPH。 所以△PHE∽△PFG,所以PG/PE=PF/PH,所以PE·PF=PG·PH。