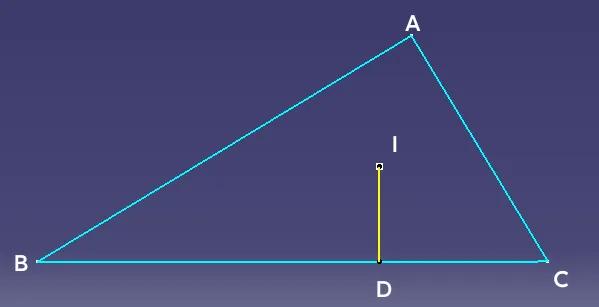
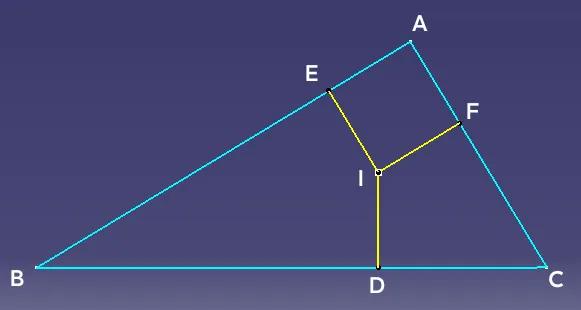
利用代数方程解几何证明题 如图一,I是△ABC的内心,ID⊥BC于D,且AB·AC=2BD·DC,求证BA⊥CA 如图二,作IE⊥AB于E,IF⊥AC于F,根据内心性质有BD=BE,AE=AF,CD=CF,设BD=x,AE=z,CD=y,角A、B、C所对边为a、b、c。 则有x+y=a,y+z=b,z+x=c,令p=(a+b+c)/2,解方程得:x=p-b,y=p-c,z=p-a。 将结果代入AB·AC=2BD·DC可得:bc=2(p-b)(p-c),化简得:2p²-2(b+c)p+bc=0。由于p>0,由求根公式可得p=(b+c)/2+√(b²+c²)/2=(a+b+c)/2,所以a²=b²+c²,所以且∠BAC=90°,即BA⊥CA。