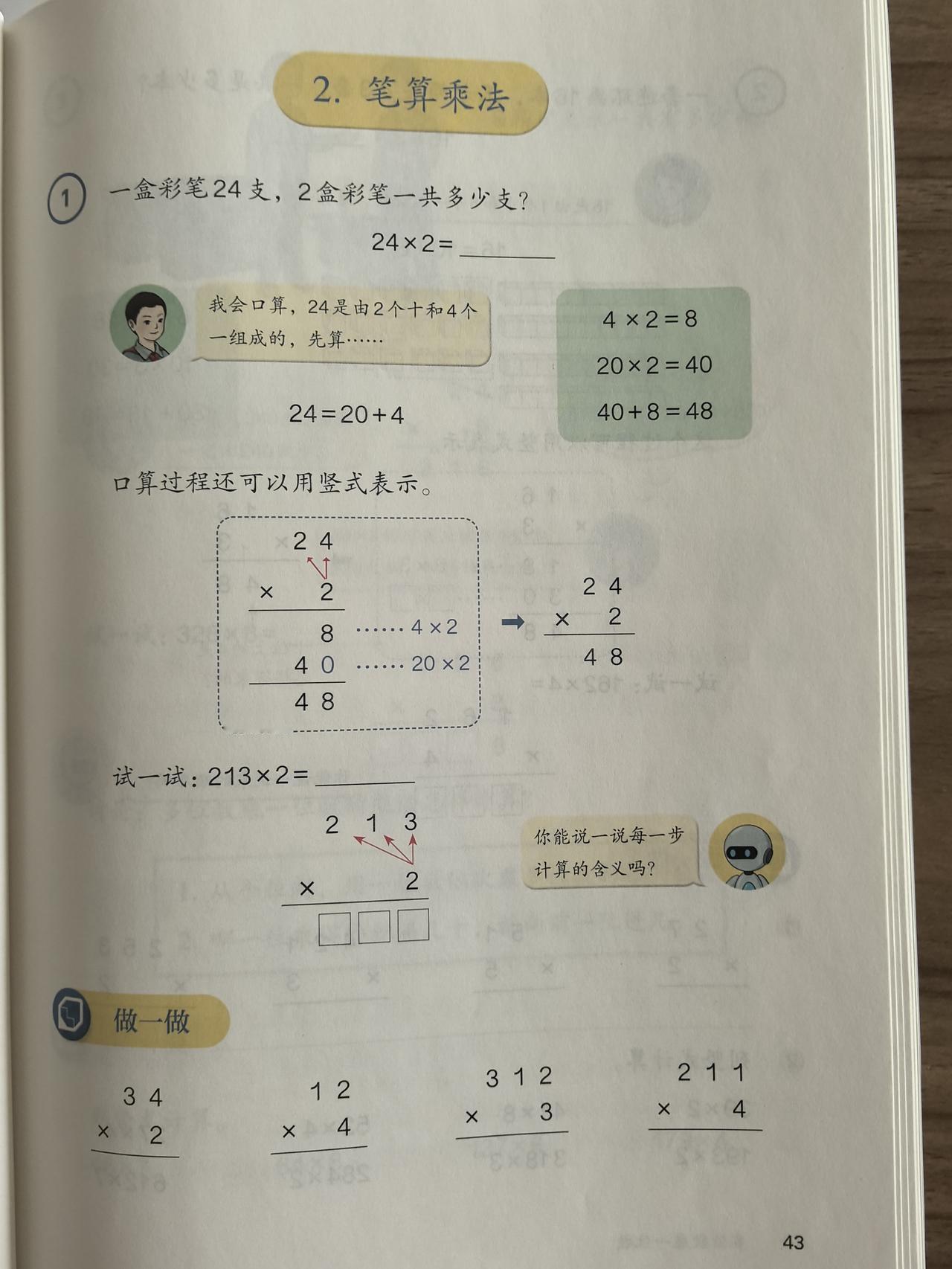
让笔算乘法的“根”与“形”自然联结——教材《笔算乘法》深度解读 一、教材内核:锚定“运算能力”与“几何直观”的双向生长 本内容属于“数与代数”领域中“多位数乘一位数”的笔算起始课,核心是让学生理解“两位数、三位数乘一位数(不进位)”的笔算算理,掌握笔算方法。同时,借助“数的拆分”与“竖式记录”的关联,培育运算能力(能规范、合理地进行笔算)与几何直观(通过竖式的“形”,理解运算的“理”)。 二、编排智慧:从“口算溯源”到“竖式建模”的逻辑进阶 (一)情境锚定:用生活需求启动数学思考 以“一盒彩笔24支,2盒共多少支”的生活问题引入,将“笔算乘法”的学习与“求总数(单价×数量)”的实际需求挂钩,让学生体会笔算的应用价值,避免运算学习的“抽象化”。 (二)算理贯通:口算与笔算的自然衔接 教材先呈现“24×2”的口算过程:将24拆分为“20+4”,分别计算“4×2=8”“20×2=40”,再“40+8=48”。这种“拆分—分别运算—合并结果”的思路,是**“数的组成”在运算中的体现**,既承接了之前“口算乘法”的方法,又为笔算的“分位相乘、累加结果”提供了算理支撑。 (三)竖式建模:从“理”到“形”的可视化表达 教材将口算过程转化为竖式: - 先算“4×2=8”,对应竖式中“个位上的4乘2,得数8写在个位”; - 再算“20×2=40”,对应竖式中“十位上的2(表示2个十)乘2,得数40,其中4写在十位”; - 最后“40+8=48”,对应竖式中“个位与十位结果的累加”。 这种“分步记录、逐步合并”的竖式设计,把抽象的“数的运算”转化为直观的“竖式结构”,让学生清晰看到“每一步计算对应数的哪一部分”,真正实现“理”(数的组成与运算)与“形”(竖式的书写形式)的统一。 (四)拓展迁移:从“两位数”到“三位数”的能力生长 “试一试:213×2”的设计,是让学生基于“两位数乘一位数”的算理与竖式经验,自主迁移到“三位数乘一位数”的学习中。通过“说一说每一步计算的含义”,推动学生思考“百位上的2(表示2个百)乘2,结果应写在百位”,从而建构“多位数乘一位数(不进位)”的通用笔算模型:从个位起,用一位数依次乘多位数的每一位数,乘到哪一位,得数的末位就和那一位对齐。 三、教学启示:让笔算乘法的学习“有理有形” (一)锚定“数的组成”,让算理“立得住” 教学时,可借助“小棒模型”强化算理感知。例如计算“24×2”时,用“2捆(每捆10根)加4根”代表24,先摆2组“4根”,算出“4×2=8”;再摆2组“2捆”,算出“20×2=40”;最后合并“40+8=48”。通过“实物操作—口算表达—竖式记录”的联动,让学生明白“竖式的每一步都是数的组成在运算中的体现”。 (二)聚焦“竖式结构”,让算法“看得见” 针对竖式教学,可设计“竖式解剖”活动:将竖式的每一行(如“8”“40”“48”)用不同颜色标注,结合小棒操作或口算步骤,让学生对应“这一行记录的是哪部分的运算”。例如用红色标注“8”,提问“这是怎么来的?对应小棒的哪部分?”,帮助学生建立“竖式步骤与数的运算”的一一对应关系。 (三)联结“迁移应用”,让能力“长得好” 在“213×2”的教学中,可先让学生尝试自主书写竖式,再组织“竖式分享会”:展示不同学生的竖式(如有的从百位开始算,有的从个位开始算),引导学生对比“哪种顺序更合理”,从而总结“从个位起依次相乘”的笔算规则。后续“做一做”的练习,要关注学生对“三位数每一位数乘一位数”的掌握,通过“说算理—写竖式—查结果”的闭环,巩固笔算模型。 数学的笔算不是机械的“符号书写”,而是“数的运算逻辑”的可视化表达。当学生能透过“24×2”的竖式,看到“2个十和4个一分别与2相乘,再合起来”的过程;能自主把这个逻辑迁移到“213×2”中,他们对乘法运算的理解,就从“会算”走向了“懂算、会教”——这正是运算素养与几何直观共生共长的美好模样。