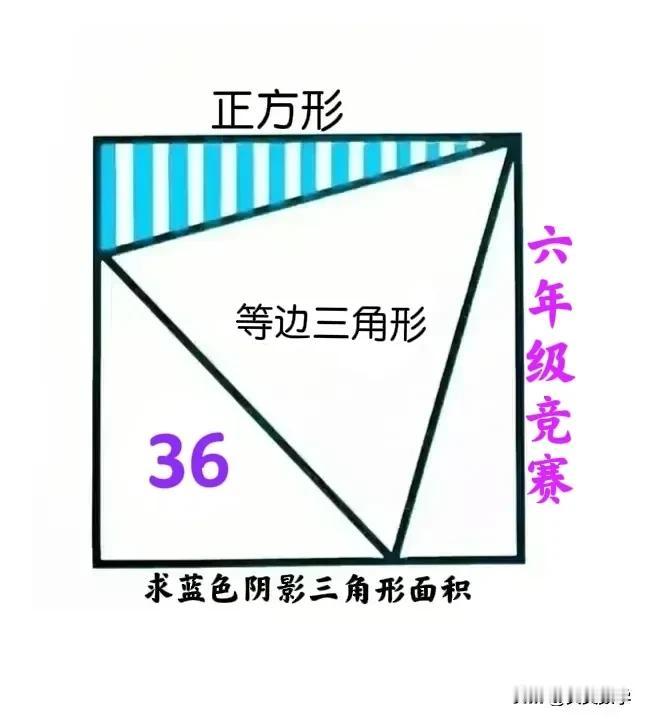
“全军覆没,学霸、尖子生无一例外!”有人说此题超纲,非使用初中知识“直角三角形内30°角对应的直角边等于斜边的一半”不可!您认为呢?这是一道小学六年级数学竞赛题: 如图,正方形被1个等边三角形,分成4个部分,左下角三角形面积为36,求阴影部分三角形的面积。 —————————— 提示:化归思想! 化归为“腰长已知、顶角为30°等腰三角形面积问题”! ①将阴影三角形绕正方形右上顶点逆时针旋转90°,恰与右侧三角形拼成1个顶角为30°的等腰三角形,其面积为阴影部分面积的2倍。 ②左下三角形必为等腰直角三角形,故其斜边长为12,从而等边三角形边长、拼成的等腰三角形的腰长均为12。 ③在拼成的等腰三角形一条腰上作高,其长度为腰的一半(无需使用初中知识“直角三角形内30°角对应的直角边等于斜边的一半”,只需将顶角为30°沿作高的腰翻折即得一等边三角形,其边长恰为高的2倍),故其面积为12×6÷2=36。 ④阴影三角形面积为36÷2=18。 友友们,怎么看?欢迎留言分享! #小学数学# #妙笔生花创作挑战#