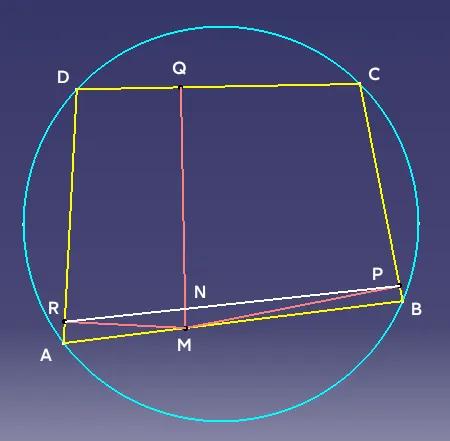
分角定理在竞赛中的应用 一道初中竞赛题:如图,ABCD是圆内接四边形,过AB上一点M引MP、MQ、MR分别垂直于BC、CD、AD。连接PR与MQ交于N,求证PN/NR=BM/MA。 分角定理内容如下:设D为△ABC的边BC所在直线上除C以外任一点,则有BD/CD=(AB·sin∠BAD)/(AC·sin∠DAC)。证明并不难,可以看我以前发的文章。 回到原题,根据圆内接四边形性质可得∠B与∠D,∠A与∠C互补,同时∠QMP与∠C互补,∠QMR与∠D互补,所∠QMP=∠A,∠QMR=∠B。 在△MRP中,根据分角定理: PN/NR=(PM·sin∠QMP)/(RM·sin∠QMR)=(PM·sin∠A)/(RM·sin∠B)=(PM/sin∠B)/(RM/sin∠A)=BM/MA。