机器之心报道
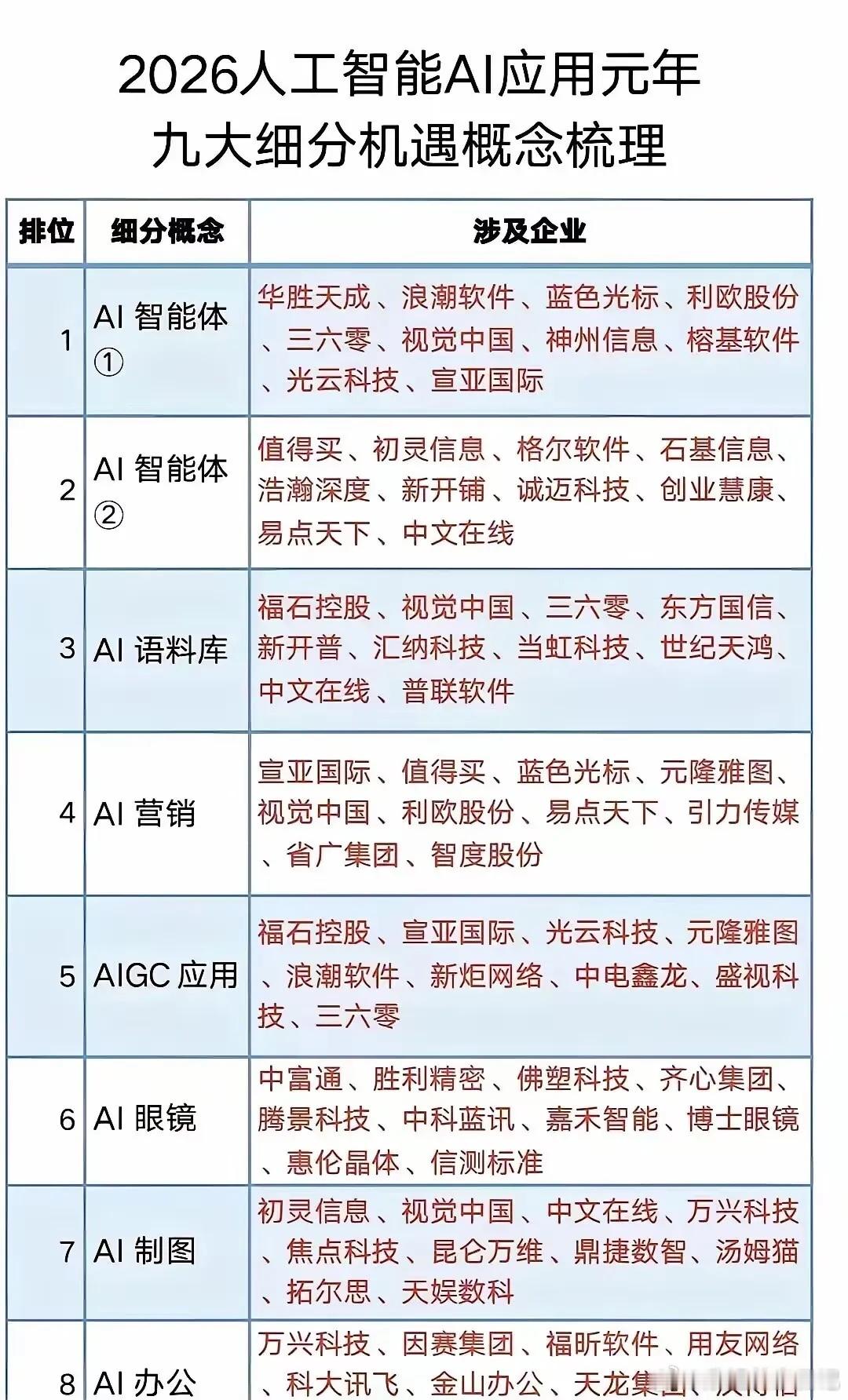
机器之心编辑部
一般来说，字越少事情越大。
数学领域的研究成果因其高门槛很少能获得广泛的关注，而这一篇却足足达到了 80 万以上的浏览量。
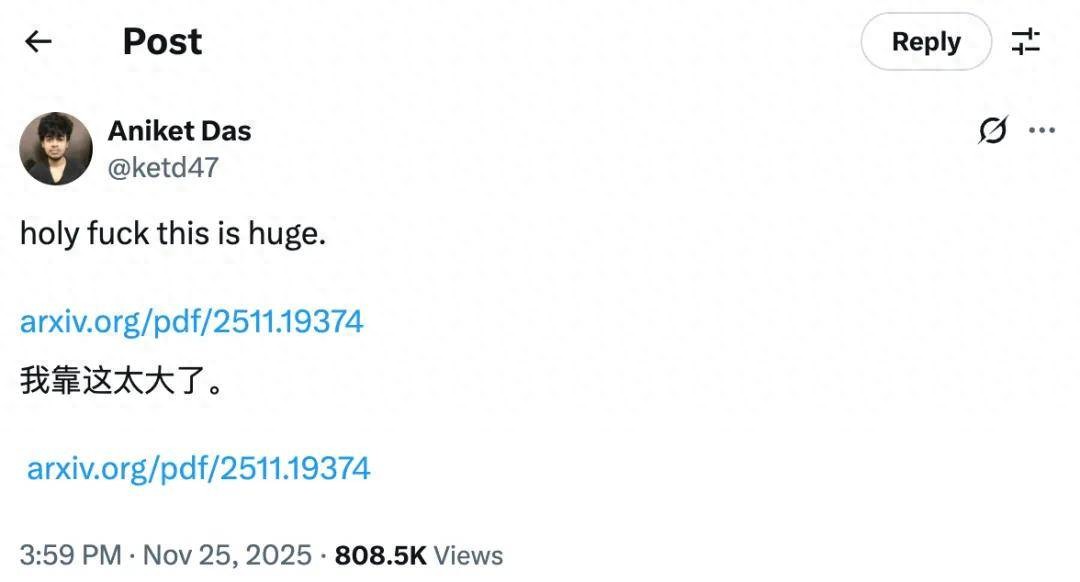
这是一篇非常硬核的数学证明论文，来自华人学者 Yuansi Chen，解决了至今已有 36 年的 Talagrand 卷积猜想的数学问题，对于现代计算机科学，机器学习等相关领域有深远的基础意义。
Yuansi Chen，ETH D-MATH 统计研讨会副教授，杜克大学统计科学系助理教授。在苏黎世 ETH 的 ETH 数据科学基础（ETH-FDS）担任博士后研究员。2023 年获得斯隆研究奖。他的研究方向聚焦于统计机器学习、MCMC 采样算法、优化方法、域适应性以及计算神经科学中的统计挑战。
论文标题：Talagrand's convolution conjecture up to loglog via perturbed reverse heat
论文链接：https://arxiv.org/abs/2511.19374 该论文证明了在布尔超立方体上的热半群 (Pτ) 下，任何非负函数 f:{−1,1} n→ℝ+ 都表现出比马尔可夫不等式更好的统一尾部界限。具体来说，对于任何 ηe3 和 τ0 ，
其中 μ 表示布尔超立方体 {−1,1}ⁿ 上的均匀测度，而 c_τ 是仅依赖于 τ 的常数。该结果在无维度依赖的情形下解决了 Talagrand 的卷积猜想，只额外损失一个 log log η 因子。其证明依赖于布尔超立方体上反向热过程的若干性质，并基于对该反向热过程进行精心设计的扰动而构造出的耦合方法。
也就是说，除了额外的 log log 因子外，Talagrand 卷积猜想的主要问题已经被解决。
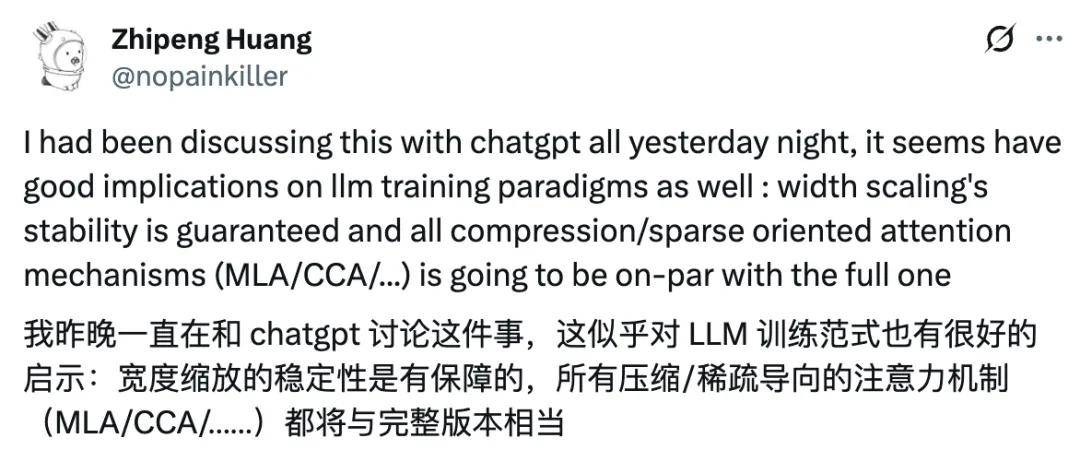
Zhipeng Huang 也进行了转发，他也在思考这一数学领域的进展对大语言模型训练的潜在影响。
背景与问题
Talagrand 卷积猜想于 1989 年首次提出，代表了概率论和泛函分析领域最重要的开放问题之一。该猜想关注热半群应用于布尔超立方体 {−1, 1}ⁿ 上的 L₁ 函数时的正则化性质。这种离散几何结构在理论计算机科学、离散数学和统计物理中都至关重要。
热半群 (Pₜ) 充当一个「平滑」算子，通过与偏置硬币测度进行卷积来定义。对于布尔超立方体上的函数 f，Pₜf (x) 表示 f 在一个点的期望值，该点是通过以 (1−e⁻ᵗ)/2 的概率独立翻转 x 的每个坐标而获得的。虽然强大的超收缩性结果保证了对 p1 的 Lₚ 函数的强正则化，但 L₁ 函数的行为仍然是个谜。
Talagrand 猜想预测，将此平滑算子应用于任何 L₁ 函数会显著改善尾部衰减 —— 具体来说，即概率 P (Pτf (X)η‖f‖₁) 应以 1/(η√log η) 的速度衰减，并且在所有维度 n 和函数 f 上都一致。这种与维度无关的性质将代表一种普遍的正则化效应，与问题的复杂性无关。在这项工作之前，尾部概率是否在 η → ∞ 时消失仍然是一个开放问题。
本文为 Talagrand 猜想建立了第一个与维度无关的上限，证明了：
定理 1：对于每个 τ0，存在一个通用常数 c0，使得对于每个非负函数 f: {−1, 1}ⁿ → R⁺ 且 ‖f‖₁ ≠ 0，以及任何 ηe³，
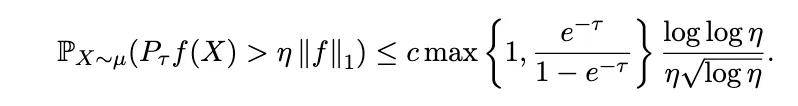
此结果解决了 Talagrand 关于
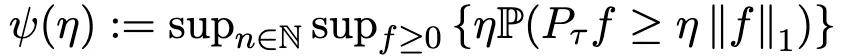
是否在 η → ∞ 时消失的基本问题，提供了肯定的答案。虽然该界限比猜想的最优速率 1/(η√log η) 多了一个 log log η 因子，但它代表了对平凡马尔可夫界限 1/η 的巨大改进，并使猜想的完全解决指日可待。
方法：扰动反向热过程
Yuansi Chen 的方法的技术核心在于通过他所谓的「扰动逆热过程」构建了两个马尔可夫跳跃过程之间复杂的耦合。这种构建代表了离散随机分析中一项重大的方法学进步。
该方法首先定义了前向和反向跳跃过程。前向过程 (Uₜ) 始于定律 νf = f・μ，其坐标以 1/2 的速率独立翻转。反向过程 (Vₜ) 是 Uₜ 的时间反演，它变为时间非均匀的，其跳跃速率取决于一个「得分函数」Sᵢ(x) := (xᵢ∂ᵢf (x))/f (x)。至关重要的是，这个得分函数充当了高斯设置中福尔默漂移的离散模拟，并保持了基本的鞅性质。
核心创新在于构建一个耦合 (Vₜ, Wₜ)，其中两个过程共享相同的泊松随机测度以实现最大相关性，但 Wₜ 在其跳跃速率中引入了一个精心设计的扰动。与可以直接扰动漂移的连续设置不同，离散设置需要通过状态依赖和坐标依赖的因子 δᵢ(x) 来扰动跳跃速率。这种扰动经过校准，以确保 Wₜ 保持在布尔超立方体上，同时实现所需的耦合性质。
技术上，证明结合了：
跳过程的鞅不等式 类 Duhamel 展式 p - 偏置的 Fourier／Parseval 分析 对梯度／得分的精细控制这些工具共同消除了此前方法中不可避免的维度依赖因素，使得在布尔超立方体上实现「无维度」控制成为可能。
在离散结构中：
噪声是跳跃型而非连续 Gaussian OU 流 对称性较弱 稀有区域（rare regimes）中必须引入更强的扰动 分布在奇异点附近缺乏连续高斯半群的光滑调和结构因此当前方法不可避免地留下一个 loglog η 的残差损失。
从连续空间到离散空间的适应带来了几个根本性的挑战，Yuansi Chen 通过创新技术解决了这些挑战：
跳跃速率与漂移扰动：直接的漂移扰动会将过程移出 {-1, 1}ⁿ，因此需要开发跳跃速率扰动方法。这导致了更复杂的状态依赖动力学，但保留了离散结构。 L₂ 距离问题：在高斯空间中有效的标准 L₂ 界在布尔超立方体上变得有问题。耦合构建专门设计为避免依赖此类界，而是通过一种新颖的多阶段方法利用总变差控制。 多阶段杜阿梅尔公式：一项关键创新涉及在多个时间间隔而不是单个阶段应用杜阿梅尔公式。这种多阶段方法被证明对于通过有效利用 Pτ 随时间的平滑性质来获得无维度界限至关重要。该证明建立了两个关键的耦合性质：Vₜ 和 Wₜ 律之间的总变差控制（引理 2），以及一个近似单调耦合性质，确保 log Pτf (Wₜ) 的大值以高概率对应于 log Pτf (Vₜ) 的更大值（引理 3）。
总结
为布尔热半群提供了几乎最优、无维度依赖的尾部正则化结果； 引入了一种全新的「反向过程耦合」技术，可应用于离散随机系统； 提升了布尔函数反集中（anti-concentration）分析的工具箱； 在离散采样、组合结构上的 score-based 生成模型等领域具有潜在外溢效应。这项工作代表了离散随机分析领域的一项里程碑式成就，成功地将复杂的连续空间技术与离散概率相结合。该界限的无维度性质对理论计算机科学具有直接影响，其中布尔超立方体在学习理论、复杂性理论和近似算法中作为基本结构。
也许最重要的是，这篇论文为彻底解决塔拉格朗猜想奠定了一条清晰的道路。剩余的 log log η 因子代表了未来研究的明确目标。作者指出，对耦合过程距离的更精细 L₂ 界或替代扰动设计可能会消除这个最终因子。
与机器学习中基于得分的生成模型的明确联系表明了潜在的跨学科影响，其中来自离散得分函数和时间反演的见解可以为离散生成模型的理论基础提供信息。
对于计算机科学家和 ML 研究员来说，这篇论文不仅仅是一个不等式的证明，它：
1. 升级了工具箱： 提供了处理高维离散空间概率分布的新工具。
2. 连接了生成模型： 其证明核心（反向热流）与当前的 AI 热点（扩散模型）在数学本质上相通。
3. 量化了正则化： 也就是为什么「平滑 / 加噪」总是能带来「好」的分布性质。
该论文将一个数十年悬而未决的开放问题转变为一个拥有明确后续步骤的活跃领域，同时增进了对离散结构上正则化效应的基本理解。这项工作既是一个重要的解决方案，引导未来深入探索连续和离散随机分析之间丰富的相互作用。
更多信息，请参阅原论文。
