2025年LLM领域有个有意思的趋势:与其继续卷模型训练,不如在推理阶段多花点功夫。这就是所谓的推理时计算(Test-Time / Inference-Time Compute):在推理阶段投入更多计算资源,包括更多Token、更多尝试、更深入的搜索,但不会改动模型权重。
ARC-AGI基准测试就是个典型案例。通过推理时技术可以达到87.5%的准确率,但代价是每个任务超过1000美元的推理成本。没用这些技术的LLM通常只能拿到不到25%。
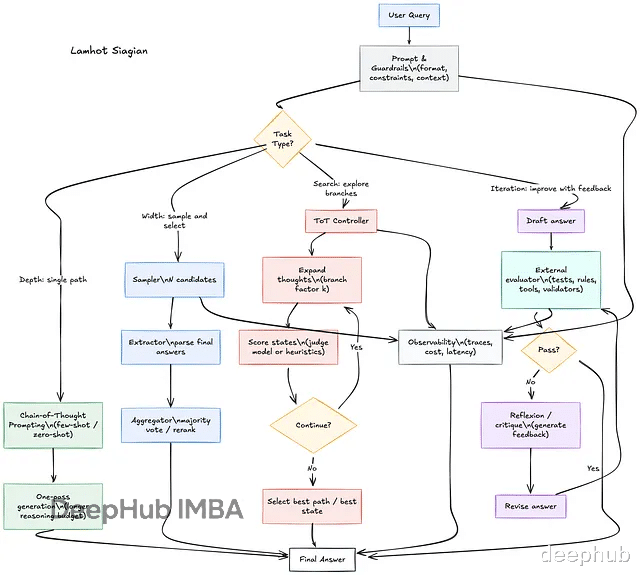
本文要讲四种主流的推理时计算技术:深度方向的Chain-of-Thought,宽度方向的Self-Consistency,搜索方向的Tree-of-Thoughts,以及迭代方向的Reflexion/Self-Refine。
预备知识:LLM调用封装先把基础设施搭好。下面是通用的LLM调用接口和辅助函数:
from collections import Counter, dequeimport re# ---- LLM调用封装 ----def llm(prompt: str, temperature: float = 0.7, max_tokens: int = 800) -> str: """ LLM调用的占位函数。 在实际使用中,可以替换为OpenAI、Claude或本地模型的API调用。 参数: prompt: 输入提示词 temperature: 采样温度,控制输出多样性 max_tokens: 最大生成token数 返回: 模型生成的文本 """ # 示例:使用OpenAI API # from openai import OpenAI # client = OpenAI() # response = client.chat.completions.create( # model="gpt-4", # messages=[{"role": "user", "content": prompt}], # temperature=temperature, # max_tokens=max_tokens # ) # return response.choices[0].message.content raise NotImplementedError("请实现你的LLM调用逻辑")# ---- 辅助函数:提取最终答案 ----def extract_final_answer(text: str) -> str: """ 从模型输出中提取最终答案。 寻找格式为 "FINAL: <答案>" 或 "Final: <答案>" 的模式。 在实际应用中,建议: - 让模型输出JSON格式,如 {"final": "..."} - 或使用针对具体任务的解析逻辑 参数: text: 模型的完整输出文本 返回: 提取的最终答案(最多200字符) """ m = re.search(r"(FINAL|Final)\s*[:\-]\s*(.*)", text) return (m.group(2).strip() if m else text.strip())[:200]
深度(Depth):链式思维推理Chain-of-Thought(CoT)是最基础也用得最多的推理时技术。核心思想很直白:让模型「思考」久一点。
传统调用方式期望模型直接给答案,但复杂问题不是这么解决的。CoT让模型生成详细的中间推理步骤,在数学、逻辑推理、编程这些任务上效果很明显。
为什么管用?首先是分解作用,大问题拆成小步骤,每一步更容易做对。其次是中间步骤充当了一种「外部记忆」,帮模型追踪推理过程。第三是强制模型展示推理,减少直接「猜」答案的情况。最后,模型推理过程中可以自查前面步骤对不对。
触发CoT有几种常见办法:零样本提示就是加一句「Let's think step by step」;少样本提示是给2-3个带推理步骤的例子;指令微调是用带CoT标注的数据集训练;系统提示则是在system message里定义推理风格。
def solve_with_cot(question: str) -> str: """ 使用链式思维(Chain-of-Thought)解决问题。 通过精心设计的提示词,引导模型: 1. 进行逐步推理 2. 展示中间计算过程 3. 最后给出明确的最终答案 参数: question: 需要解答的问题 返回: 包含推理过程和最终答案的完整响应 """ prompt = f"""You are a careful reasoner. Your task is to solve the following problem.Instructions:1. Break down the problem into smaller steps2. Show your reasoning for each step3. Double-check your calculations4. End with a clear final answerFormat your response as:Step 1: [your first step]Step 2: [your second step]...FINAL: <your final answer>Question: {question}""" # 使用较低的temperature以获得更确定性的输出 return llm(prompt, temperature=0.2, max_tokens=900)# 使用示例if __name__ == "__main__": question = "一个农场有鸡和兔,共35个头和94只脚。请问有多少只鸡和多少只兔?" result = solve_with_cot(question) print(result) print("\n提取的最终答案:", extract_final_answer(result))
CoT适合数学应用题、逻辑推理、代码调试、规划任务这类需要多步计算的问题。简单事实问答用CoT有点浪费,创意写作也不太合适——过度结构化会限制发挥。
局限性也很明显。Token消耗会上升,输出越长成本越高。模型可能在推理链中犯错,错误还会传播。输出格式也不总是稳定,需要后处理。
宽度(Width):自洽性采样Self-Consistency的想法很简单:与其相信单次输出,不如生成多个答案,选最一致的那个。
有点像集体决策——单条推理链可能出错,但如果多条独立路径都指向同一答案,那答案八成是对的。
这方法管用的原因:单次采样可能因为随机性出错,多次采样能平均掉这些错误。正确答案往往能通过多条不同路径得到。不同路径可能捕捉问题的不同侧面。答案的一致性程度还顺便反映了模型的「信心」。
做Self-Consistency有几个关键决策要做。
第一是采样多样性。这点至关重要。如果所有采样都走同一条推理路径,自洽性就没意义了。高多样性设置是temperature 0.7-0.9、top_p 0.9-0.95,加上多样的提示词变体。temperature太低或提示词太固定都不行。
第二是采样数量。3-5个边际收益最高,适合成本敏感场景;10-20个是常规配置;40个以上适合对准确率要求极高的场景,但边际收益已经很低了。
第三是聚合策略。最常用的是多数投票,选出现次数最多的答案。也可以加权投票,根据置信度加权。还可以把相似答案聚类后再投票。
def solve_with_self_consistency( question: str, n: int = 10, temperature: float = 0.8) -> dict: """ 使用自洽性(Self-Consistency)方法解决问题。 通过高温度采样生成多个多样化的答案, 然后通过多数投票选择最一致的答案。 参数: question: 需要解答的问题 n: 采样数量,建议10-20 temperature: 采样温度,建议0.7-0.9以确保多样性 返回: 包含以下键的字典: - final: 最终答案(得票最多的) - votes: 该答案的得票数 - confidence: 置信度(得票数/总数) - all_finals: 所有提取的答案列表 - vote_distribution: 完整的投票分布 - samples: 所有原始输出(用于调试) """ prompt_template = """Solve this problem step by step. Show your reasoning, then end with 'FINAL: ...'Question: {question}""" samples = [] for i in range(n): out = llm( prompt_template.format(question=question), temperature=temperature, # 高温度确保多样性 max_tokens=900 ) samples.append(out) # 提取所有最终答案 finals = [extract_final_answer(s) for s in samples] # 统计投票 vote_counter = Counter(finals) most_common = vote_counter.most_common() winner = most_common[0] return { "final": winner[0], "votes": winner[1], "confidence": winner[1] / n, "all_finals": finals, "vote_distribution": dict(vote_counter), "samples": samples }def solve_with_weighted_consistency( question: str, n: int = 10, score_fn=None) -> dict: """ 带权重的自洽性方法。 除了多数投票外,还可以根据每个答案的质量分数加权。 参数: question: 需要解答的问题 n: 采样数量 score_fn: 评分函数,接受(question, answer)返回0-1的分数 返回: 包含加权投票结果的字典 """ samples = [] for _ in range(n): out = llm( f"Solve step by step. End with 'FINAL: ...'\n\nQ: {question}", temperature=0.8, max_tokens=900 ) samples.append(out) finals = [extract_final_answer(s) for s in samples] # 加权投票 weighted_votes = {} for final, sample in zip(finals, samples): weight = score_fn(question, sample) if score_fn else 1.0 weighted_votes[final] = weighted_votes.get(final, 0) + weight winner = max(weighted_votes.items(), key=lambda x: x[1]) return { "final": winner[0], "weighted_score": winner[1], "weighted_distribution": weighted_votes, "all_finals": finals }# 使用示例if __name__ == "__main__": question = "如果今天是星期三,那么100天后是星期几?" result = solve_with_self_consistency(question, n=10) print(f"最终答案: {result['final']}") print(f"得票数: {result['votes']}/{len(result['all_finals'])}") print(f"置信度: {result['confidence']:.1%}") print(f"投票分布: {result['vote_distribution']}")
Self-Consistency适合有确定答案的问题(数学、编程、事实问答)、答案空间有限的问题(选择题、是/否问题)、以及生产环境中需要高可靠性的场景。开放式问题答案空间太大,每次答案都不同,投票没意义。创意任务没有「正确」答案可投票,也不适用。
局限性:成本线性增长,N次采样就是N倍成本。如果模型系统性地偏向某个错误答案,投票也救不了。同一答案的不同表述可能被当作不同答案,答案标准化是个麻烦事。
搜索(Search):思维树探索Tree-of-Thoughts(ToT)把推理过程当成搜索问题来做。每个节点是一个「思维状态」,也就是部分推理结果;每条边是一个「思维步骤」,即推理动作;目标是找到通向正确答案的路径。
跟线性的CoT不同,ToT允许分支(从一个状态探索多个可能的下一步)、回溯(放弃没希望的分支,回到之前的状态)、评估(判断当前状态离目标有多近)。
为什么有效?线性推理一旦犯错就没法恢复,ToT可以回溯。某些问题天然是树形结构,比如博弈、规划。通过评估函数引导搜索,避免盲目探索。只深入探索有希望的分支,Token利用率更高。
搜索策略有几种选择。BFS广度优先,逐层探索,不会错过浅层解但内存消耗大。DFS深度优先,一条路走到底,内存效率高但可能陷入死胡同。Beam Search每层保留top-k状态,平衡效率和覆盖,但可能丢失最优解。A*用启发式函数引导,最优且高效,但需要好的启发函数。MCTS蒙特卡洛树搜索能处理大搜索空间,但需要大量模拟。
def tot_bfs( question: str, max_depth: int = 4, beam: int = 3, branch: int = 4, external_evaluator=None) -> dict: """ 使用BFS策略的思维树(Tree-of-Thoughts)方法。 工作流程: 1. 从空状态开始 2. 对当前frontier中的每个状态,生成多个可能的下一步 3. 评估所有新状态 4. 保留得分最高的beam个状态作为新frontier 5. 重复直到达到最大深度 6. 从最佳状态生成最终答案 参数: question: 需要解答的问题 max_depth: 最大搜索深度 beam: 每层保留的状态数(beam width) branch: 每个状态扩展的分支数 external_evaluator: 外部评估函数(可选), 接受(question, state)返回分数 返回: 包含以下键的字典: - final_text: 最终答案 - best_state: 最佳推理状态 - best_score: 最佳状态的分数 - search_tree: 搜索过程的记录(用于可视化) """ def propose_next_steps(state: str) -> list: """ 给定当前推理状态,生成多个可能的下一步。 """ prompt = f"""You are exploring different ways to solve a problem.Question: {question}Current reasoning state:{state if state else "(Starting from scratch)"}Propose {branch} different possible next steps to continue the reasoning.Each step should be a distinct approach or calculation.Return as a numbered list:1. [first possible step]2. [second possible step]...""" raw = llm(prompt, temperature=0.9, max_tokens=400) # 解析编号列表 steps = [] for line in raw.splitlines(): line = line.strip() if line and line[0].isdigit(): # 移除编号前缀 step = line.split(".", 1)[-1].strip() if step: steps.append(step) return steps[:branch] if steps else [raw.strip()] def llm_score_state(state: str) -> float: """ 使用LLM评估一个推理状态的promising程度。 注意:在实际应用中,使用外部评估器(如单元测试、规则检查) 通常比LLM自我评估更可靠。 """ if external_evaluator: return external_evaluator(question, state) prompt = f"""Evaluate how promising this partial solution is.Question: {question}Current reasoning state:{state}Consider:1. Is the reasoning logical and correct so far?2. Is it making progress toward a solution?3. Are there obvious errors or dead ends?Rate from 0 to 10 (10 = very promising, likely to lead to correct answer).Output only a number.""" s = llm(prompt, temperature=0.0, max_tokens=10).strip() try: return float(re.findall(r"\d+(\.\d+)?", s)[0]) except: return 5.0 # 默认中等分数 # 初始化 frontier = [""] # 初始状态为空 best_state = "" best_score = -1.0 search_tree = [] # 记录搜索过程 for depth in range(max_depth): candidates = [] depth_record = {"depth": depth, "states": []} for state in frontier: next_steps = propose_next_steps(state) for step in next_steps: # 构建新状态 new_state = (state + "\n" + step).strip() # 评估新状态 score = llm_score_state(new_state) candidates.append((score, new_state)) depth_record["states"].append({ "state": new_state[:200] + "..." if len(new_state) > 200 else new_state, "score": score }) search_tree.append(depth_record) # 排序并保留top-k candidates.sort(reverse=True, key=lambda x: x[0]) frontier = [s for _, s in candidates[:beam]] # 更新最佳状态 if candidates and candidates[0][0] > best_score: best_score, best_state = candidates[0] # 从最佳状态生成最终答案 final_prompt = f"""Based on the reasoning below, produce the final answer.Question: {question}Reasoning:{best_state}Provide a clear, concise final answer.End with: FINAL: <your answer>""" final = llm(final_prompt, temperature=0.2, max_tokens=400) return { "final_text": final, "final_answer": extract_final_answer(final), "best_state": best_state, "best_score": best_score, "search_tree": search_tree }def tot_dfs( question: str, max_depth: int = 5, branch: int = 3, threshold: float = 3.0) -> dict: """ 使用DFS策略的思维树方法。 通过深度优先搜索探索解决方案空间, 当某个分支的分数低于阈值时进行剪枝。 参数: question: 需要解答的问题 max_depth: 最大搜索深度 branch: 每个状态扩展的分支数 threshold: 剪枝阈值,分数低于此值的分支被放弃 返回: 包含最终答案和搜索路径的字典 """ best_result = {"state": "", "score": -1.0} visited_count = [0] # 使用列表以便在嵌套函数中修改 def propose_steps(state: str) -> list: prompt = f"""Propose {branch} next reasoning steps.Question: {question}Current state:{state if state else "(empty)"}Return as numbered list.""" raw = llm(prompt, temperature=0.9, max_tokens=300) steps = [l.split(".", 1)[-1].strip() for l in raw.splitlines() if l.strip()[:1].isdigit()] return steps[:branch] if steps else [raw.strip()] def score_state(state: str) -> float: prompt = f"""Rate this partial solution 0-10.Question: {question}State: {state}Output only a number.""" s = llm(prompt, temperature=0.0, max_tokens=10).strip() try: return float(re.findall(r"\d+(\.\d+)?", s)[0]) except: return 5.0 def dfs(state: str, depth: int): visited_count[0] += 1 if depth >= max_depth: score = score_state(state) if score > best_result["score"]: best_result["state"] = state best_result["score"] = score return for step in propose_steps(state): new_state = (state + "\n" + step).strip() score = score_state(new_state) # 剪枝:跳过低分分支 if score < threshold: continue if score > best_result["score"]: best_result["state"] = new_state best_result["score"] = score dfs(new_state, depth + 1) dfs("", 0) # 生成最终答案 final = llm( f"""Produce final answer based on:Question: {question}Reasoning: {best_result['state']}End with FINAL: ...""", temperature=0.2 ) return { "final_text": final, "final_answer": extract_final_answer(final), "best_state": best_result["state"], "best_score": best_result["score"], "states_visited": visited_count[0] }# 使用示例if __name__ == "__main__": question = "使用数字1, 5, 6, 7(每个只能用一次),通过加减乘除得到24。" result = tot_bfs(question, max_depth=3, beam=2, branch=3) print("=== BFS Tree-of-Thoughts ===") print(f"最佳推理路径:\n{result['best_state']}") print(f"\n最佳分数: {result['best_score']}") print(f"\n最终答案: {result['final_answer']}")
ToT适合组合问题(24点游戏、数独)、规划任务、博弈问题(象棋、围棋)、头脑风暴这类需要探索不同方向的场景。答案空间极大时可能需要配合启发式剪枝。简单问题用不着——直接CoT就够了。
局限性:计算成本高昂,需要大量LLM调用来评估和扩展节点。LLM自评估不太可靠,评估函数质量直接决定效果。实现复杂度比其他几种方法高不少。还有些问题压根没有明显的树形结构,ToT就不太适用。
迭代(Iteration):反思与自我改进Reflexion和Self-Refine用的是经典的「生成-评估-改进」循环:模型先产生初始答案,拿到反馈后修正答案,如此反复直到满意或达到最大轮数。
人类学习不也是这样吗?很少有事情一次就做对,总是通过反馈不断改进。
但有个重要的坑要注意:没有可靠外部反馈的「自我纠正」可能适得其反。
研究表明,模型仅靠自己判断来「自我纠正」时,可能把正确答案改成错误答案,可能对错误判断过度自信,可能在无效修改上浪费Token。
所以最佳实践是尽量用外部反馈源。代码执行(单元测试、错误信息)和规则检查(格式验证、约束检查)最可靠。工具调用(计算器、搜索引擎)和人类反馈也不错。另一个LLM做交叉验证勉强能用。同一个LLM自评效果最差,缺乏外部参照。
def self_refine( question: str, score_fn, rounds: int = 3, improvement_threshold: float = 0.1) -> dict: """ 使用自我改进(Self-Refine)方法迭代优化答案。 核心流程:生成 -> 评估 -> 根据反馈改进 -> 重复 参数: question: 需要解答的问题 score_fn: 评估函数,签名为: score_fn(answer_text) -> (score: float, feedback: str) - score: 0.0-1.0之间的分数 - feedback: 具体的改进建议 强烈建议使用外部评估器! rounds: 最大改进轮数 improvement_threshold: 最小改进阈值,低于此值则提前停止 返回: 包含以下键的字典: - final: 最终答案 - final_score: 最终分数 - history: 完整的改进历史 - rounds_used: 实际使用的轮数 """ # 生成初始答案 initial_prompt = f"""Provide a thoughtful answer to this question.Show your reasoning and end with FINAL: ...Question: {question}""" answer = llm(initial_prompt, temperature=0.4) history = [] prev_score = -float('inf') for round_num in range(rounds): # 评估当前答案 score, feedback = score_fn(answer) history.append({ "round": round_num + 1, "answer": answer, "score": score, "feedback": feedback }) # 检查是否有足够的改进 if round_num > 0 and (score - prev_score) < improvement_threshold: # 如果改进不明显,考虑提前停止 if score >= prev_score: pass # 继续,至少没有退步 else: # 退步了,恢复上一个答案 answer = history[-2]["answer"] score = history[-2]["score"] break # 如果分数已经很高,提前停止 if score >= 0.95: break prev_score = score # 根据反馈改进答案 refine_prompt = f"""Improve your answer based on the feedback below.Question: {question}Your current answer:{answer}Feedback (score: {score:.2f}/1.00):{feedback}Instructions:1. Keep what is correct in your current answer2. Fix the issues mentioned in the feedback3. Make sure not to introduce new errors4. End with FINAL: ...Improved answer:""" answer = llm(refine_prompt, temperature=0.3) # 最终评估 final_score, final_feedback = score_fn(answer) return { "final": answer, "final_answer": extract_final_answer(answer), "final_score": final_score, "history": history, "rounds_used": len(history) }# ---- 示例评估函数 ----def make_code_evaluator(test_cases: list): """ 创建一个代码评估函数。 参数: test_cases: 测试用例列表,每个元素是(input, expected_output) 返回: 评估函数 """ def evaluator(code_answer: str) -> tuple: # 提取代码块 code_match = re.search(r"```python\n(.*?)```", code_answer, re.DOTALL) if not code_match: return 0.0, "No Python code block found. Please wrap your code in ```python ... ```" code = code_match.group(1) passed = 0 failed_cases = [] for inp, expected in test_cases: try: # 危险:实际应用中应使用沙箱! local_vars = {} exec(code, {"__builtins__": {}}, local_vars) # 假设代码定义了solve函数 if 'solve' in local_vars: result = local_vars['solve'](inp) if result == expected: passed += 1 else: failed_cases.append(f"Input: {inp}, Expected: {expected}, Got: {result}") else: return 0.0, "No 'solve' function found in your code." except Exception as e: failed_cases.append(f"Input: {inp}, Error: {str(e)}") score = passed / len(test_cases) if failed_cases: feedback = "Failed test cases:\n" + "\n".join(failed_cases[:3]) # 最多显示3个 if len(failed_cases) > 3: feedback += f"\n... and {len(failed_cases) - 3} more failures" else: feedback = "All test cases passed!" return score, feedback return evaluatordef make_math_evaluator(correct_answer): """ 创建一个数学答案评估函数。 参数: correct_answer: 正确答案 返回: 评估函数 """ def evaluator(answer_text: str) -> tuple: extracted = extract_final_answer(answer_text) # 尝试数值比较 try: extracted_num = float(re.findall(r"-?\d+\.?\d*", extracted)[0]) correct_num = float(correct_answer) if abs(extracted_num - correct_num) < 0.01: return 1.0, "Correct!" else: return 0.0, f"Incorrect. Your answer: {extracted_num}, Expected: {correct_num}" except: pass # 字符串比较 if extracted.lower().strip() == str(correct_answer).lower().strip(): return 1.0, "Correct!" else: return 0.0, f"Incorrect. Your answer: {extracted}, Expected: {correct_answer}" return evaluatordef make_llm_evaluator(criteria: str): """ 创建一个基于LLM的评估函数(不推荐作为唯一评估源)。 参数: criteria: 评估标准描述 返回: 评估函数 """ def evaluator(answer_text: str) -> tuple: prompt = f"""Evaluate this answer based on the following criteria:Criteria: {criteria}Answer to evaluate:{answer_text}Provide:1. A score from 0.0 to 1.02. Specific feedback on what's wrong and how to improveFormat:SCORE: [number]FEEDBACK: [your feedback]""" response = llm(prompt, temperature=0.0) try: score = float(re.search(r"SCORE:\s*([\d.]+)", response).group(1)) score = min(1.0, max(0.0, score)) except: score = 0.5 try: feedback = re.search(r"FEEDBACK:\s*(.+)", response, re.DOTALL).group(1).strip() except: feedback = response return score, feedback return evaluator# 使用示例if __name__ == "__main__": # 示例1:代码任务 question = "编写一个函数solve(n),返回n的阶乘。" test_cases = [ (0, 1), (1, 1), (5, 120), (10, 3628800) ] result = self_refine( question=question, score_fn=make_code_evaluator(test_cases), rounds=3 ) print("=== Self-Refine for Code ===") print(f"最终分数: {result['final_score']:.2%}") print(f"使用轮数: {result['rounds_used']}") print(f"\n改进历史:") for h in result['history']: print(f" Round {h['round']}: score={h['score']:.2f}") # 示例2:数学任务 question = "计算 17 * 23 + 45 - 12" correct = 17 * 23 + 45 - 12 result = self_refine( question=question, score_fn=make_math_evaluator(correct), rounds=2 ) print("\n=== Self-Refine for Math ===") print(f"最终答案: {result['final_answer']}") print(f"正确答案: {correct}") print(f"最终分数: {result['final_score']:.2%}")
Self-Refine适合代码生成(有单元测试作为外部反馈)、格式化任务(有明确规范可检查)、约束满足问题(可验证约束是否满足)、事实核查(可通过检索验证)。主观任务需要人类反馈或多模型交叉验证。没有反馈来源时别用——纯LLM自评不靠谱。
局限性:反馈质量决定上限,垃圾反馈只会导致垃圾改进。模型有时候会在不同版本之间来回「改」,出现震荡。每轮迭代都消耗Token,成本会累积。也无法保证收敛——模型可能根本没法利用反馈真正改进。
技术对比与选择指南四种技术各有特点。CoT思考更深,Token消耗低,LLM只调用一次,实现简单,不需要外部反馈,适合推理链问题。Self-Consistency采样更广,Token消耗中等,LLM调用N次,实现也简单,不需要外部反馈,适合有确定答案的问题。ToT探索更多,Token消耗高,LLM调用次数是分支数乘以深度,实现复杂,外部反馈可选但推荐,适合组合和规划问题。Self-Refine改进更好,Token消耗中等,LLM调用次数是轮数乘以2,实现复杂度中等,强烈推荐外部反馈,适合可迭代改进的问题。
选择思路如下,需要分步推理就先试CoT,不稳定的话加上Self-Consistency。有确定答案且需要可靠性,直接用Self-Consistency。组合或搜索问题用ToT。有外部反馈源就用Self-Refine。不确定用什么就先用CoT,看效果再定。
这些技术可以组合使用。CoT加SC是每次采样都用CoT然后多数投票。ToT加SC是ToT生成多个最终答案用SC选择。ToT加SR是用SR迭代改进ToT的最佳结果。复杂任务可能需要把多种技术串成流水线。
def combined_approach(question: str, score_fn) -> str: """ 组合使用多种推理时技术。 流程: 1. 用ToT探索解决方案空间 2. 用Self-Consistency从多个ToT结果中选择 3. 用Self-Refine迭代改进最终答案 """ # 第一阶段:ToT探索(运行3次) tot_results = [] for _ in range(3): result = tot_bfs(question, max_depth=3, beam=2, branch=3) tot_results.append(result['final_answer']) # 第二阶段:Self-Consistency选择 vote = Counter(tot_results).most_common(1)[0][0] # 第三阶段:Self-Refine改进 final_result = self_refine( question=question, score_fn=score_fn, rounds=2 ) return final_result['final_answer']
实践建议别一上来就用最复杂的技术。推荐的顺序是:先直接提问作为baseline,然后加CoT提示,再加Self-Consistency,最后才考虑ToT或Self-Refine。
对于Self-Refine和ToT,评估器质量直接决定效果。花时间构建好的评估器比调参更重要。
推理时技术能大幅提升性能,但成本也会大幅增加。建议设置Token预算上限,记录每个任务的实际消耗,根据任务重要性调整投入。
部署到生产环境前做A/B测试,找到最佳的性能/成本权衡点。
总结推理时计算技术代表了LLM能力释放的新范式。在推理阶段多投入一些计算,同一个模型不重新训练就能有明显提升。本文介绍的四种技术——CoT、Self-Consistency、Tree-of-Thoughts、Self-Refine——各有特点和适用场景。理解原理和局限性,选择合适的技术或组合,是LLM应用开发的关键技能。
随着这一领域的发展,会有更多创新的推理时技术出现。但核心原则不会变:给模型更多「思考」的空间,让它展示真正的推理能力。
https://avoid.overfit.cn/post/2bb5bb4e569a4687a272dc6e9fe6809a