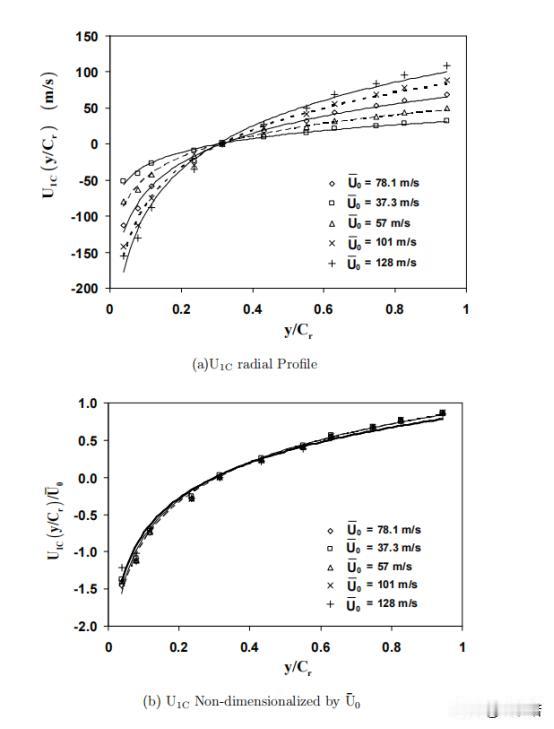
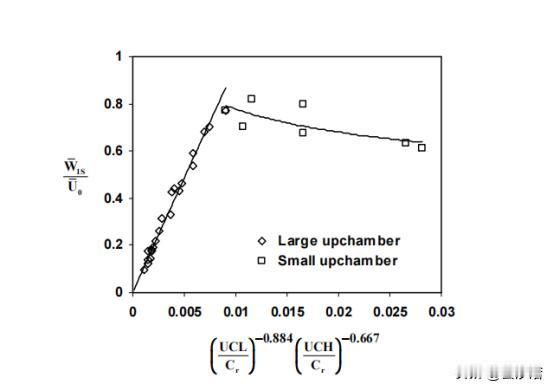
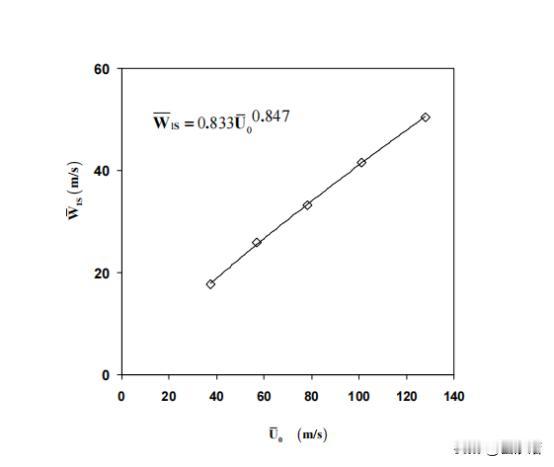
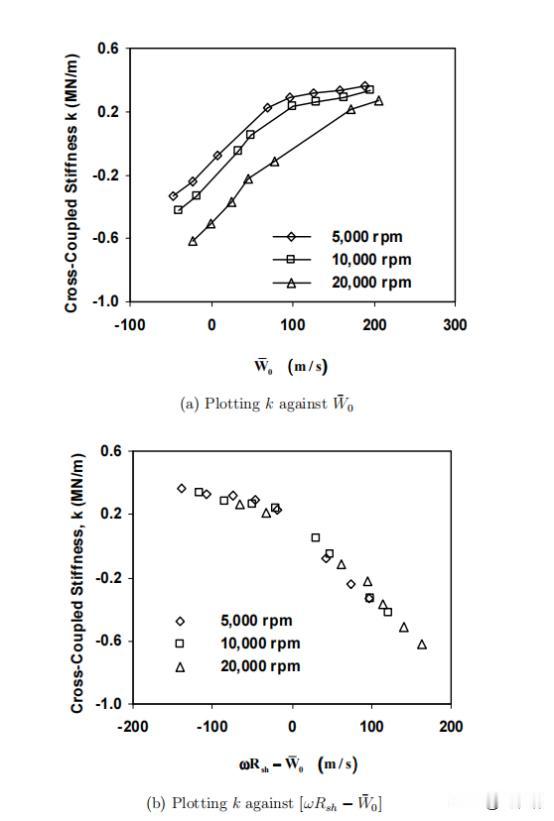
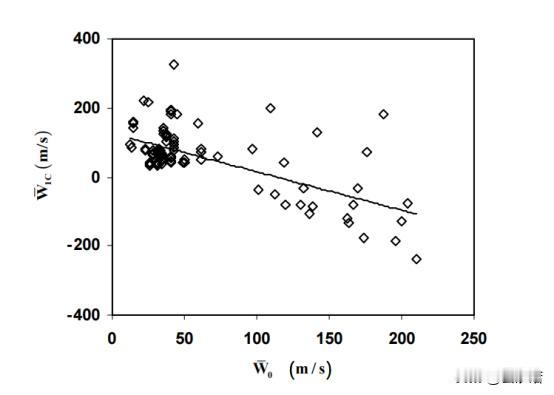
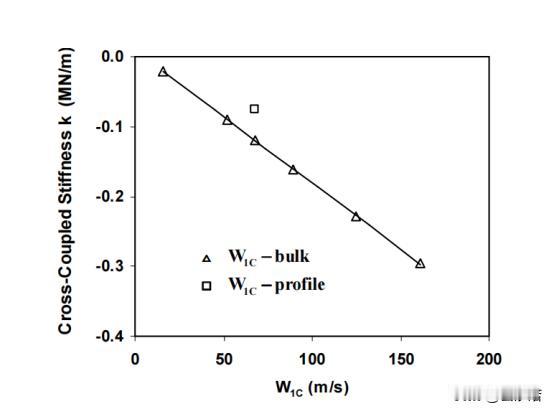
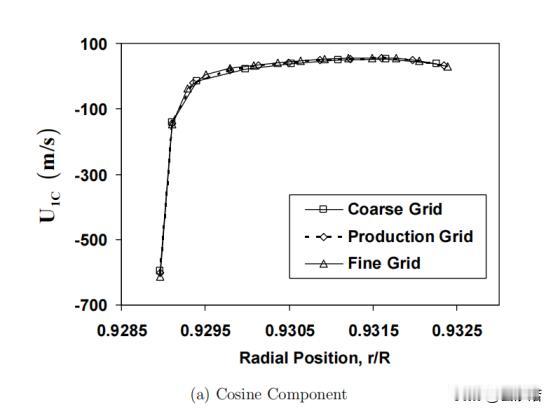
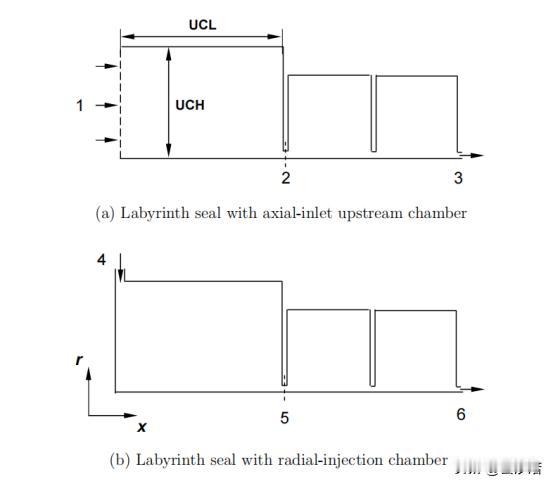
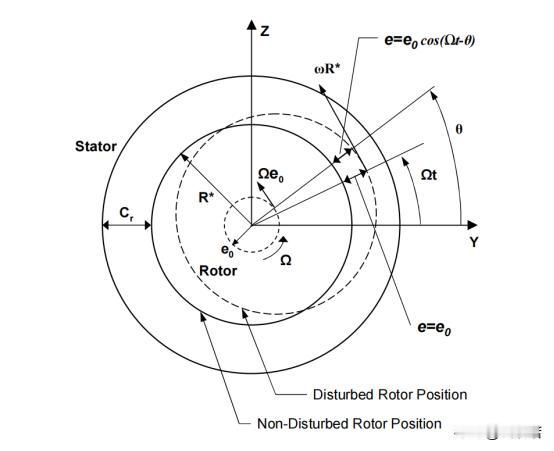
如何在偏心密封间隙中流场中,利用CFD技术进行流体动量的分离转化 前言:流体力学作为一个广泛的学科,涵盖了从大气和海洋流动到工程应用中的各种流体流动。当涉及到流体力学研究和工程应用时,理解流体流动的复杂性和动态行为,并通过探讨扰动旋转源在流体力学中的作用将变的尤为重要。 然而,某些情况下,扰动旋转源在流体流动中可能会受到扰动源的影响,这就会导致流动的不稳定性和复杂性。为了更好地理解和预测这些复杂的流体行为,数值模拟方法,特别是CFD技术,已成为不可或缺的工具。 而CFD技术在偏心密封间隙中,中流场的特征以及相关的数学方程涵盖了涡轮机械密封中的流体动力学问题,探讨了流场的特性、控制方程和相关概念。 偏心密封间隙中的流场特点表现为非稳定、三维和湍流。然后,引入了用于描述该流动的控制方程,即静止参考系中的雷诺平均、湍流纳维尔-斯托克斯方程和连续性方程。这些方程用于描述流体动量的变化和流体的连续性。 雷诺应力是描述流动湍流特性的关键,它在圆柱坐标系中给出,有效湍流粘性(µe)在捕捉流动湍流行为方面起着重要作用。它定义为层流粘度和湍流粘度之和,其中后者受到湍流参数k(湍动能)和ε(湍流能耗散率)的影响。 在湍流方面,采用了k-ε湍流,该关注湍动能(k)和湍流能耗散(ε)。这些方程有助于预测湍流行为及其与流场的相互作用。方程中的常数,如c1、c2、σk和σε,影响湍流的准确性,并根据实验数据进行校准。 研究还采用了状态方程来考虑流体的可压缩性。该方程将压力(P)、密度(ρ)、温度(T)和流体的压缩因子(γ)联系起来。在处理可压缩流体时,这一步骤是至关重要的,它允许更准确地表示流体行为。 我们假设转子围绕外壳的中心位置做圆周运动,其轨道半径远小于密封间隙。鉴于获得迷宫式密封瞬态三维计算流体动力学解的复杂性,此处采用的方法利用了边界(径向间隙)呈现时间和圆周周期性的观察结果。 为了处理这种情况,提出了转子表面位置的分解。位移的旋翼表面可以分成一个稳定的轴对称部分和一个小的非稳定的非对称部分。轴对称部分代表未受干扰的表面位置,而非稳定部分说明转子的小偏心率,并产生周期性流动干扰。 这种分解可通过以下等式获得:R(\theta,t)= r^*+\εr _ e \ cdot c_re^{j(\omega t-\ theta)}R(θ,t)=R∗+ϵReC rej(Ωt−θ)这里,R^*R代表同心转子表面位置,\epsilonϵ是一个小参数,R_eRe代表转子的偏心率,C_rCr是一个系数,jj是虚数单位,\欧米茄Ω是转子运动的角频率,\thetaθ是角度位置,以及tt是时间。 这种方法假设各种流动特性,如速度、压力和密度,也可以分成稳定的轴对称部分和非稳定的非对称部分。这些属性的一般表达式如下所示:\Phi(x,r,\theta,t) = \Phi_0(x,r)+\εr_e^n \ hat { \ phi } _ 1(x,r)e^{j(\Omega t - \theta)}Φ(x,r,θ,t)=Φ0(x,r)+ϵRenΦ^1(x,r)ej(Ωt−θ)。 在这个等式中,\PhiΦ代表流体流量变量,\epsilon = e / C_rϵ=e/Cr, ee是转子偏心率,以及\hat{\Phi}_1Φ^1是一个复杂的一阶变量,描述x - rx−r空间。该方程表明,转子的小偏心率会产生周期性的气流扰动。 气流扰动的余弦和正弦分量代表2D函数x - rx−r不同圆周位置的平面,这种方法适用于转子位移幅度相对于外壳中心线非常小的情况。假设紊流粘性、紊流动能和紊流能量耗散不会受到轻微转子位移的显著影响,通过将分解的表达式代入控制方程,最终可以导出零阶和一阶方程。 总结:我们通过实验,介绍了偏心密封间隙中流场的特性和相关数学方程,以及如何通过数值模拟方法来研究复杂的流体力学问题,而偏心密封间隙中流场的研究不仅对涡轮机械密封领域具有重要意义,还有望在更广泛的工程和科学领域产生深远影响。 相信不久的将来,随着计算能力的增强,可以考虑更精确的数值模拟方法,以更准确地捕捉偏心密封间隙中流场的复杂特性,再加上研究和应用的不断深化,我们可以更好地理解和利用流体力学的原理,为未来的技术创新和工程应用做出贡献。